ANSWER
The area of the forest after 13 years is 1,11758km^2
Step-by-step explanation
Given that;
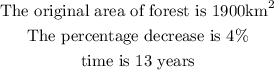
Follow the steps below to find the area of the forest after 13 years
Since the size of the forest decreases every year by 4%, then apply the below formula
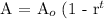
Where
A is the area of the forest after some years
Ao is the original area of the forest
r is the interest rate
t is the time
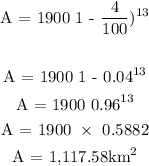
Therefore, the area of the forest after 13 years is 1,11758km^2