The standard deviation is:
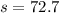
The confidence interval is 95%
You want to be confident that your estimate is within 10 of the true population mean, then you can use the next formula:
![ME=z\frac{s}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/biebbzgc1hhho2f2ikdup4y4djo1lfpk15.png)
Where ME is the marginal error, z is the z-score (for a confidence interval of 95% is 1.96), s is the standard deviation and n the sample size.
Then, by replacing the values:
![\begin{gathered} 10=1.96\frac{72.7}{\sqrt[]{n}} \\ 10*\sqrt[]{n}=1.96\frac{72.7}{\sqrt[]{n}}*\sqrt[]{n} \\ 10*\sqrt[]{n}=1.96*72.7 \\ \sqrt[]{n}=(1.96*72.7)/(10) \\ \sqrt[]{n}=14.2492 \\ \sqrt[]{n}^2=14.2492^2 \\ n=203.04 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/n8vfemtv5ffo9r8be45dbhgxzf8nmqad8a.png)
Thus, you need a sample size of at least 204 people.