For the first right triangle
the points of the hypotenuse
(0,3)=(x1,y1)
(7,0)=(x2,y2)
the slope of the hypotenuse is
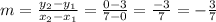
and the equation of the hypotenuse
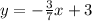
For the second triangle
The points of the hypotenuse
(0,9)
(21,0)
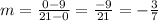
and the equation of the hypotenuse
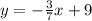
The equations are not equal but they have the same slope, which indicates that the equations are parallels.
The answer is
No, because one is larger than the other