Question

Abby took an 8-question multiple-choice quiz. Suppose that her probability of correctly answering any question is 0.75. What is Abby's probability of incorrectly answering exactly two questions on the quiz?

Answer 1

We have to find the probability of incorrectly answering exactly 2 questions on the quiz.

As the quiz has 8 questions, this means that incorrectly anwering exactly 2 questions malso tell us that the other 6 questions were answered correctly.

The probability of correctly answering any question is constant and has a value of p = 0.75.

Then, we can model the amount of correct answers as a binomia random variable witht n = 8 (the numbe of questions) and p = 0.75.

We can calculate then the probability of correcly answering 6 questions, which is an equivalent event to incorrectly answer 2 questions:

`\begin{gathered} P(x=k)=\binom{n}{k}p^k(1-p)^(n-k) \\ \\ P(x=2)=(8!)/(2!6!)\cdot0.75^6\cdot0.25^2 \\ \\ P(x=2)\approx28\cdot0.1780\cdot0.0625 \\ \\ P(x=2)\approx0.3115 \end{gathered}`

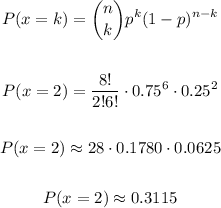
We can check this answer as:

Answer: the probbility is 0approximately .3115.