The Solution:
Given that an amount of money is compounded yearly at 10% interest.
We are required to find how many years it will take the money to double.
By the Compound Interest formula,
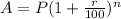
Part a:
In this case,
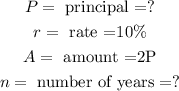
Substituting these values in the formula, we get
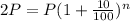
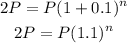
Dividing through by P, we get
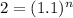
Taking the logarithm of both sides, we get
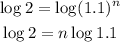
Dividing both sides by log1.1, we get
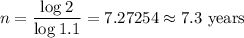
Therefore, it will take approximately 7.3 years to double your money.
Part b:
Compounded weekly.
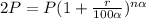
In this case,
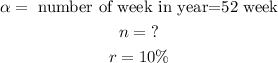
Substituting, we get
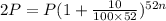
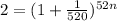
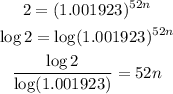
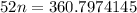
Dividing both sides, we get
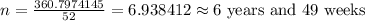
Thus, it will take approximately 6 years and 49 weeks to double your money.
Part c:
Compounded continuously, which I suppose means compounded daily.
Recall:
365 days = 1 year
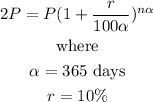
Substituting these values, we get
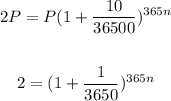

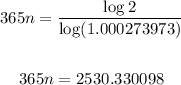
Dividing both sides by 365, we get
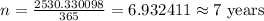
Therefore, it will take approximately 7 years to double your money.