Question

Hi, can you help me answer this question please, thank you!

Answer 1

a) Given the hypotheses:

`\begin{gathered} H_0\colon p_1=p_2 \\ H_a\colon p_1\\e p_2 \end{gathered}`

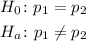
You have to conduct the hypotheses test using a level of significance of α=0.02.

This is a test for the difference of proportions, the test statistic is an approximation to the standard normal distribution with the following formula:

`Z_(H0)=\frac{(\hat{p_1}-\hat{p_2})-(p_1-p_2)}{\sqrt[]{\lbrack\hat{p}(1-\hat{p})\rbrack((1)/(n_1)+(1)/(n_2))}}`

Where

p-hat 1 is the sample proportion of the first population

p-hat 2 is the sample proportion of the second population

p-hat is the overall sample proportion

First, you have to calculate the sample proportions:

Sample 1

n₁=299 (successes + failures)

x₁= 30 (nº of successes)

The sample proportion is equal to the quotient between the number of successes and the sample size:

`\begin{gathered} \hat{p_1}=(x_1)/(n_(1)) \\ \hat{p_1}=(30)/(299) \\ \hat{p_(1)}=0.10 \end{gathered}`

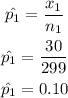
Sample 2

n₂= 484 (successes + failures)

x₂= 18 (nº of successes)

Calculate the sample proportion:

`\begin{gathered} \hat{p_(2)}=(x_(2))/(n_(2)) \\ \hat{p_(2)}=(18)/(484) \\ \hat{p_(2)}=0.037\approx0.04 \end{gathered}`

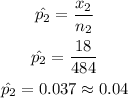
Overall sample proportion

To calculate the sample proportion between both samples you have to add the number of successes of both samples and both sample sizes and then divide the results, following the formula:

`\hat{p}=(x_1+x_2)/(n_1+n_2)`
`\begin{gathered} \hat{p}=(30+18)/(299+484) \\ \hat{p}=(48)/(783) \\ \hat{p}=0.061 \\ \hat{p}=0.06 \end{gathered}`

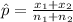
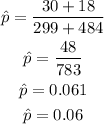
Now you can calculate the value of the test statistic, remember, under the null hypotheses the difference between the population proportions is considered to be zero:

`p_1-p_2=0`

The test statistic can be calculated as follows:

`\begin{gathered} Z_(H0)=\frac{(0.1-0.04)-0}{\sqrt[\square]{0.6(1-0.6)((1)/(299)+(1)/(484))}} \\ Z_(H0)=\frac{0.06}{\sqrt[]{0.6\cdot0.4\cdot(783)/(144716)}} \\ Z_(H0)=(0.06)/(0.036) \\ Z_(H0)=1.665 \end{gathered}`

The test statistic is Z= 1.665

b) The p-value is the probability of obtaining a value as extreme as the value of the test statistic under the null hypotheses.

This test is two-tailed, which means that you can reject the null hypotheses to small values of Z or to high values of Z. To find the p-value you have to determine the corresponding probability:

`\begin{gathered} p-\text{value}=\text{ P(Z}\leq-1.665)+P(Z\ge1.665) \\ p-\text{value}=P(Z\leq-1.665)+(1-P(Z\leq1.665)) \\ p-\text{value}=0.04796+(1-0.95204) \\ p-\text{value}=0.04796+0.04796 \\ p-\text{value}=0.09592\approx0.0959 \end{gathered}`

The p-value is 0.0959

c) The p-value of 0.0959 is greater than the level of significance α=0.02.

The decision will be to not reject the null hypothesis.