We need to solve the equation:
![x=2+\sqrt[]{x-2}](https://img.qammunity.org/2023/formulas/mathematics/college/p86j57wn4rlanmtb69fb8wrgkrpi84ss3o.png)
First, we can subtract 2 from both sides of the equation and then square both sides:

Now, we apply some operations on both sides to obtain:
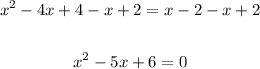
And we can apply the quadratic formula to obtain the solutions. Notice, though, that x-2 cant be negative because this expression was originally inside the square root. So, we have the following condition for the solution:
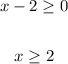
Now, using the quadratic formula, we obtain:
![\begin{gathered} x=\frac{5\pm\sqrt[]{(-5)^(2)-4(1)(6)}}{2(1)} \\ \\ x=\frac{5\pm\sqrt[]{25-24}}{2} \\ \\ x=\frac{5\pm\sqrt[]{1}}{2} \\ \\ x=(5\pm1)/(2) \\ \\ x_1=(5-1)/(2)=2 \\ \\ x_2=(5+1)/(2)=3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a5cen44uz4bhncg9t14j8fku9qcxkwj5jk.png)
Therefore, since both solutions satisfy the condition imposed by the square root, the solutions are
x = 2 and x = 3