Question

Runner A is initially 8.4 km west of a flagpole and is running with a constant velocity of 2.6 km/h due east. Runner B is initially 5.4 km east of the flagpole and is running with a constant velocity of 8.6 km/h due west. What will be the distance of the two runners from the flagpole when their paths cross? ____km from the flagpole due from which of the following: west, east, north or south?

Answer 1

First, let's make a diagram to visualize the problem.

We know that, at the start, runners are 13.8 kilometers apart. So, the distance of runner A is going to be x, while the distance of runner B is going to be 13.8-x. Then, we use the equation of constant motion.

`t=(d)/(v)`

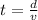
Let's express an equation for each runner using the given velocities and the expressions of the distances we defined before.

`\begin{gathered} A\colon t=(x)/(2.6) \\ B\colon t=(13.8-x)/(8.6) \end{gathered}`

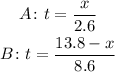
Now we combine the equations to solve for x.

The distance of Runner A is 3.2 km.

Then, we subtract to find the position with respect to the flagpole.

Therefore, they will be 5.2 km west.