Question

Classify each angle pair as corresponding, alternate interior, alternate exterior, or consecutive interior angles.123145 67189 1011/1213 141516a Z1 and Z9b. Z6 and 215C. 22 and 251d 23 and 2101:: Corresponding Angles:: Alternate Interior Angles:: Alternate Exterior Angles:: Consecut

Answer 1

So the classification is:

a: Alternate Interior Angles

b: Corresponding Angles

c: Alternate Interior Angles

d: Consecutive Interior Angles

Based on the image you've provided, we can classify the angle pairs as follows:

1. Corresponding Angles: These are pairs of angles that are in the same relative position at each intersection where the transversal crosses the two lines. Typically, one of these angles is on the interior and the other is on the exterior, but they are on the same side of the transversal.

2. Alternate Interior Angles: These are pairs of angles that are on opposite sides of the transversal and inside the two lines.

3. Alternate Exterior Angles: These are pairs of angles that are on opposite sides of the transversal and outside the two lines.

4. Consecutive Interior Angles (or Same-Side Interior Angles): These are pairs of angles that are on the same side of the transversal and inside the two lines.

Let's classify each pair given in the image:

- Pair a (angle 4 ) and (angle 9 ): These angles are on opposite sides of the transversal and both on the interior of the two lines, making them alternate interior angles.

- Pair b (angle 6 ) and (angle 15 ): (angle 6 ) is on the interior and
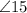`\( \angle 15 \)`is on the exterior, and they are on the same side of the transversal but different lines, making them corresponding angles.

- Pair c
`(\( \angle 2 \)` and
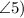`\( \angle 5 \))`: These angles are on opposite sides of the transversal and both on the interior of the two lines, making them alternate interior angles.

- Pair d
`(\( \angle 3 \)` and
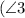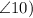`\( \angle 10 \))`: These angles are on the same side of the transversal and both on the interior of the two lines, making them consecutive interior angles.

Answer 2

According to the given graph, we have the following:

• Angles 1 and 9 are ,corresponding angles.

,

• Angles 6 and 15 are ,alternate exterior angles.

,

• Angles 2 and 5 are ,consecutive interior angles.

,

• Angles 3 and 10 are ,alternate interior angles.