Solution
9 (a) Using product rule

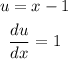
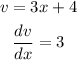
The product rule formula is quoted below
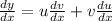

9(b) Verifying the resuts of 9(a) by bexpanding the product first and subsequently differentiating
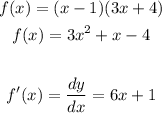
In conclusion , we observe that the results of the derivatives are the same irrespective of the approach used as shown in 9(a) and 9(b) above