Question

check all that Apply Solution to the system of inequalities shown below:x+y<=5+2 y>2a. (1,1)b. (2,5)c. (5,2)d. (3,6)e. (2,-5)f. (1,-1)

Answer 1

D. (2, 5)

Step-by-step explanation:

Given the below inequalities;

`\begin{gathered} x+y\leq5+2 \\ y>2 \end{gathered}`

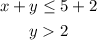
To be able to determine the solution to the above inequalities, let's go ahead and pick each of the given options and see which one is the correct answer.

A. (5, 2), x = 5 and y = 2;

Substituting we'll have;

`\begin{gathered} 5+2\leq5+2 \\ 2>2 \end{gathered}`

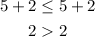
Since the 2nd equation isn't true, then option A isn't the correct option.

Let's try option D: (2, 5), x = 2 and y = 5.

Substituting, we'll have;

`\begin{gathered} 2+5\leq5+2 \\ 5>2 \end{gathered}`

We can see that (2, 5) satisfies both inequalities, therefore option D is the correct option.