Question

Use slope to determine if lines AB and CD are parallel, perpendicular, or neither 3. A(-1,8), B(2. 6), C(-1,2), D(3,3)m(AB) m(CD)Types of Lines

Answer 1

That's awesome.

Please, let me know how I did by rating our session.

Enjoy the rest of your day!ANSWER

The two lines are neither parallel nor perpendicular

Step-by-step explanation

To solve the question, we have to find the slopes of line AB and CD and then compare them.

If the two slopes are equal, the lines are parallel.

If the two slopes are the negative inverse of one another, they are perpendicular.

If they are neither of the two, then they are not related.

To find the slope, we use formula:

`slope\text{ = }\frac{y_2-y_1_{}}{x_2-x_1}`

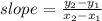
For line AB:

`\begin{gathered} (x1,\text{ y1) = (-1, 8)} \\ (x2,\text{ y2) = (2, 6)} \\ \Rightarrow\text{ slope = }\frac{6\text{ - 8}}{2\text{ - (-1)}}\text{ = }\frac{6\text{ - 8}}{2\text{ + 1}} \\ \text{slope = }(-2)/(3) \end{gathered}`

For line CD:

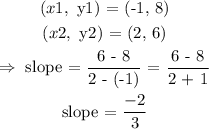
`\begin{gathered} (x1,\text{ y1) = (-1, 2)} \\ (x2,\text{ y2) = (3, 3)} \\ \Rightarrow\text{ slope = }\frac{3\text{ - 2}}{3\text{ - (-1)}}\text{ = }\frac{3\text{ - 2}}{3\text{ + 1}} \\ \text{slope = }(1)/(4) \end{gathered}`

Since the two slopes are neither the same or the negative inverse of one another, then the two lines are neither parallel nor perpendicular.