1 Answer

DatForis · Answer 1 · 2023-03-30T16:55:45+0000

The volume formula of a cylinder is :

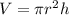
$V=\pi r^2h$

The volume formula of a cone is :

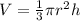
$V=(1)/(3)\pi r^2h$

From the problem, the heights are constant or the same.

So we can let h = 1 and compare the volumes.

a. Cylinder with r = 6 and h = 1

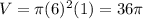
$V=\pi(6)^2(1)=36\pi$

b. Cone with r = 6 and h = 1

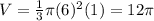
$V=(1)/(3)\pi(6)^2(1)=12\pi$

c. Cone with r = 3 and h = 1

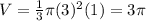
$V=(1)/(3)\pi(3)^2(1)=3\pi$

d. Cylinder with r = 3 and h = 1

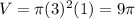
$V=\pi(3)^2(1)=9\pi$

Comparing the volumes from least to greatest :

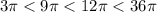
$3\pi<9\pi<12\pi<36\pi$

or c, d, b then a.

ANSWER :

C, D, B then A

Please log in or register to add a comment.