Question

In the Disney movie Tangles, Rapunzel uses her very long hair to swing out of her tower. If her hair has a length of 25 feet and rapunzel’s mass us 51kg, what is the tension in her hair if she’s moving at a velocity of 6.5 m/s at the bottom of the swing path?

Answer 1

782.58 N

Step-by-step explanation:

By the second law of Newton, at the bottom of the swing path, the net force is equal to

`\begin{gathered} F_(net)=T-mg=ma \\ \\ T-mg=m(v^2)/(r) \end{gathered}`

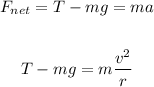
Since a is the centripetal acceleration, we get that a = v²/r. Where v is the speed and r is the length of the hair.

Solving for the tension T, we get:

`T=m(v^2)/(r)+mg`

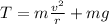
Now, we can replace m = 51 kg, v = 6.5 m/s, g = 9.8 m/s² and we can convert r = 25 feet to meters as

`25\text{ feet}*\frac{1\text{ m}}{3.281}=7.62\text{ m}`

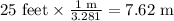
Then, the tension is equal to

`\begin{gathered} T=(51\text{ kg\rparen}\frac{(6.5\text{ m/s\rparen}^2}{7.62\text{ m}}+(51\text{ kg\rparen\lparen9.8 m/s}^2) \\ \\ T=782.58\text{ N} \end{gathered}`

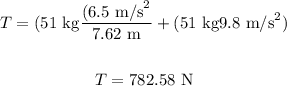
Therefore, the tension is 782.58 N