Question

How much money will you have after 5, 10, 15 & 20 weeks of savings .

Answer 1

We will have the points (0, 50) & (2, 100), using this we can find a linear equation that models the money over time. We first find the slope:

`m=(100-50)/(2-0)\Rightarrow m=25`

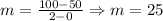
Now, using one of the points we replace in:

`y-y_1=m(x-x_1)`

We will use (0, 50), but we could use any other point of the line. Now, we replace:

`y-50=25(x-0)`

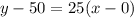
And now, we solve for y:

`\Rightarrow y=25x+50`

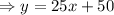
Now, in order to get the saving for each month, we replace x by 5, 10, 15 & 20 respectively:

*5 weeks:

`y=25(5)+50\Rightarrow y=175`

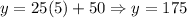
*10 weeks:

`y=25(10)+50\Rightarrow y=300`

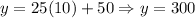
*15 weeks:

`y=25(15)+50\Rightarrow y=425`

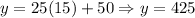
*20 weeks:

`y=25(20)+50\Rightarrow y=550`

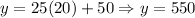
From this, we have that the savings for 5, 10, 15 & 20 weeks are 175, 300, 425 & 550 respectively.