Question

Is y = -x - 8 and y = -x + 3 perpendicular

Answer 1

Two lines are perpendicular if and only if their slopes fullfil:

`m_1m_2=-1`

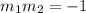
Then we need to find the slopes of each line. We notice that both lines are written in the slope intercerpt form:

`y=mx+b`

Equation y=-x-8.

Comparing this equation with the general one given above we have that:

`m_1=-1`

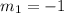
Equation y=-x+3

Comparing this equation with the general one given above we have that:

`m_2=-1`

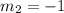
Plugging this values in the condition we have that:

`m_1m_2=(-1)(-1)=1`

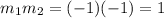
Since the result is not -1 we conclude that the condition is not fullfil, therefore the lines are not perpendicular between each other.