Question

A graph of position versus time for a certain particle moving along the x-axis is shown in the figure below. Find the average velocity in the following time intervals.A coordinate plane has a horizontal axis labeled t (s) and a vertical axis labeled x (m). The horizontal axis ranges from 0 to 8 s and the vertical axis ranges from −6 m to 10 m.A line enters the viewing window from the origin and moves up and to the right at a constant slope until it reaches (2, 10).The line then moves down and to the right until it reaches (4, 5).The line then moves horizontally to the right until it reaches (5, 5).The line then moves down and to the right until it reaches (7, −5).The line then moves up and to the right until it reaches (8, 0).(a) 0 to 2.00 s m/s(b) 0 to 4.00 s m/s(c) 2.00 s to 4.00 s m/s(d) 4.00 s to 7.00 s m/s(e) 0 to 8.00 s m/s

Answer 1

From the given position-time graph, let's find the average velocity in the following time intervals.

To find the average velocity for each time interval, apply the formula:

`v=(x_2-x_1)/(t_2-t_1)`

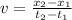
Let's solve for the following:

• (a). From 0 to 2.00 s.

When t = 0, x = 0

When t = 2.00, x = 10 m

Thus, we have:

`\begin{gathered} v=(10-0)/(2.00-0) \\ \\ v=(10)/(2.00) \\ \\ v=5.0\text{ m/s} \end{gathered}`

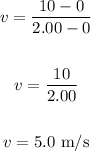
The average velocity over this time interval is 5.0 m/s

• (b). 0 to 4.00 s

When t = 0, x = 0

When t = 4.00, x = 5.0

Thus, we have:

`\begin{gathered} v=(5.0-0)/(4.0-0) \\ \\ v=(5)/(4) \\ \\ v=1.25\text{ m/s} \end{gathered}`

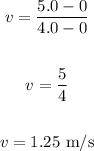
The average velocity over this time interval is 1.25 m/s.

• (c). From 2.00 s to 4.00s

When t = 2.00s, x = 10m

When t = 4.00s, x = 5m

Thus, we have:

`\begin{gathered} v=(5-10)/(4.00-2.00) \\ \\ v=(-5)/(2) \\ \\ v=-2.5\text{ m/s} \end{gathered}`

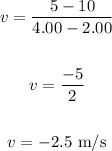
The average velocity over this time interval is -2.5 m/s.

• (d). From 4.00s to 7.00s:

When t = 4.00s, x = 5m

When t = 7.00s, x = -5 m

Thus, we have:

`\begin{gathered} v=(-5-5)/(7.00-4.00) \\ \\ v=(-10)/(3.00) \\ \\ v=-3.33\text{ m/s} \end{gathered}`

The average velocity over this time interval is -3.33 m/s.

• (e). From 0 to 8.00 s.

When t = 0, x = 0

When t = 8.00s, x = 0

Thus, we have:

`\begin{gathered} v=(0-0)/(8.00-0) \\ \\ v=(0)/(8) \\ \\ v=0\text{ m/s} \end{gathered}`

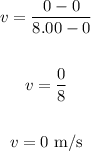
The average velocity over this time interval is 0 m/s.

ANSWER:

• (a). 5.0 m/s

,

• (b). 1.25 m/s

,

• (c). -2.5 m/s

,

• (d). -3.33 m/s

,

• (e). 0 m/s