Question

UsetheBinomialProbabilityFormulatofindtheprobabilityofobtainingexactlyone“2” afterrollingafairdie6times.

Answer 1

P(X = x) = 0.401

Step-by-step explanation

We want to use Binomial Probability to find out the probability of obtaining exactly one 2 after rolling a fair die 6 times.

The Binomial Probaility method involves the use of the formula:

`P(X=x)=^nC_x\cdot p^x\cdot q^{n\text{ - x}}`

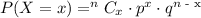
where n = number of trials in the experiment

x = number of successes in the experiment

p = probability of success in one trial

q = probability of failure in one trial

In this experiment, success would be getting a 2 in one roll of the die.

This means that, from the question:

n = 6

x = 1

p = 1/6 (probability of success in rolling a number from a die is always 1/6)

q = 5/6

Note: C means combination

So, we have that:

`\begin{gathered} P(X=x)=^6C_1\cdot\text{ (}(1)/(6))^1\cdot\text{ (}(5)/(6))^{6\text{ - 1}} \\ P(X\text{ = x) = }\frac{6!}{(6\text{ - 1)!1!}}\cdot\text{ }(1)/(6)\cdot\text{ (}(5)/(6))^5 \\ P(X\text{ = x) = 6 }\cdot\text{ }(1)/(6)\cdot\text{ }(3125)/(7776) \\ P(X\text{ = x) = 0.40} \end{gathered}`

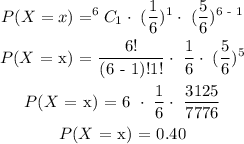
That is the probability of rolling exactly one 2 after 6 times.