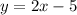Given for problem 3:
We will find the equation of the line that passes through the points
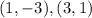
The slope-intercept form is: y = m * x + b
where (m) is the slope, and (b) is the y-intercept
The slope will be calculated as follows:
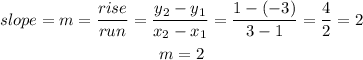
So, the equation will be:
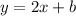
Substitute with (1, -3) and m = 2
The solve for b
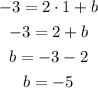
so, the answer will be the equation of the line is: