ANSWER:
0.195
Explanation:
Given:
p = 58% = 0.58
Sample size (n) = 50
We can calculate the mean and standard deviation as follows:
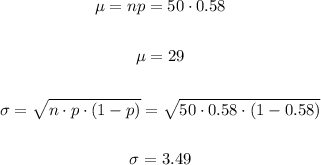
Now we must calculate the probability of at least 32, therefore:
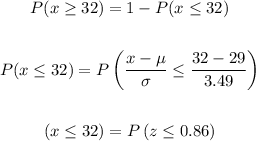
We use the normal table to determine the probability, like this:
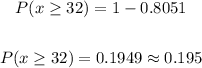
Therefore, the correct answer is 0.195