We need to purchase 4 packs of pencils and 4 packs of pens.
A pack of pencils costs $3. This means that to purchase four packs, we can multiply the cost of one pack by the number of packs we want to purchase.
$3.00 + $3.00 + $3.00 + $3.00 = $12.00
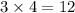
However, the distributive property can be completed by using the formula a(b + c), where a is the factor you want to multiply both by.
Since a pack of pencils is $3 and a pack of pens is $5, we can create an expression where a is 4 (this is the amount of packs we want for both pens and pencils), and b and c are the price of a pack of pencils and the price of a pack of pens.

Then, we will use the distributive property, which states that a(b + c) equals ab + ac. This means we multiply a and b and add the product of a and c to it.

Therefore, to purchase 4 packs of pencils and 4 packs of pens, it will cost $32. Let's check our work:
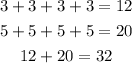
We still reach 32 dollars, so the final answer is $32. This is determined with 4(3 + 5).