Th given equation of a line is in the slope intercept form;
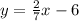
where the slope(m) is 2/7 and the intercept is -6.
For any line to be perpendicular to the above, its slope must be equal to the negative reciprocal of the slope of the line y= 2/7x – 6.
The reciprocal of the slope of y= 2/7x – 6 is -7/2.
So, let's go ahead and check each of the given lines to see which one has a slope of -7/2;
For line 2x + 7y = -56.
Let's write this in the slope intercept form;
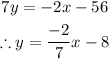
The slope here is -2/7 which is not the required answer.
Let's pick the 7x - 2y = 6,
Writing this in the slope intercept form, we'll have;
![undefined]()