The number of free throws, and the points he makes has a binomial distribution with the parameters n(amount of free throws) and p(probability to make the free throw).
From the text, those parameters are
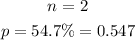
The expectation of the binomial distribution is given by
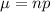
Using our values on this formula, we have
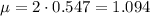
The expected value of points is 1.094.