Question

. The probability of eating pizza for dinner on Friday is 65% and the probability of going to bed early on Friday is 58%. The probability of going to bed early on Friday given that you eat pizza for dinner is 82%. What is the probability of eating pizza on Friday given that you go to bed early on Friday?

Answer 1

The Bayes' Theorem is used to calculate conditional probabilities, that is, the probability of occurrence of an event given another event has already occurred.

The formula is:

`P(A|B)=(P(B|A)* P(A))/(P(B))`

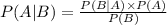
Let's call:

Event A = Eat pizza for dinner

Event B = Go to bed early

We are given the following probabilities:

P(A) = 65% = 0.65

P(B) = 58% = 0.58

P(B|A) = 82% = 0.82

Substituting:

`P(A|B)=(0.82*0.65)/(0.58)=0.9190`

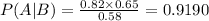
Answer: 91.90%