Question

Use the fundamental identities to find the value of the trigonometric function.Find sin θ, given that cos 2θ = _ and tan θ < 0. 3

Answer 1

Consider the following information:

`\cos (\theta)=(2)/(3)`

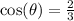
and

`\tan (\theta)<0`

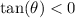
by definition, this means that:

`\cos (\theta)=(2)/(3)=\frac{adjacent\text{ side}}{hypotenuse}`

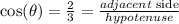
now, to find sin(θ), we must first apply the Pythagorean theorem to find the opposite side:

`\text{opposite side = }\sqrt[]{3^2-2^2}\text{ = }\sqrt[]{5}`

now, since tan θ < 0 and cos θ > 0, then, the angle must be in the second quadrant, thus sin θ < 0 and it is:

`\sin (\theta)=-\frac{opposite\text{ side}}{hypotenuse}=-\frac{\sqrt[]{5}}{3}`

So that, we can conclude that the correct answer is:

`-\frac{\sqrt[]{5}}{3}`