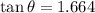Question

Suppose csc(theta) = 7/6 and cos(theta) < 0. Use a trig identity to find the value of tan(theta).

Answer 1

Given:

`\begin{gathered} csc\theta=(7)/(6) \\ \\ \cos \theta<0 \end{gathered}`

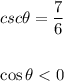
Let's use a trig identity to find the value of tanθ.

Apply the definition of cosecant to find known sides of the unit circle.

We have:

`\csc \theta=(hypotenuse)/(opposite)=(7)/(6)`

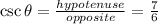
Here, the hypotenuse and opposite sides are known.

Also, find the adjacent side using Pythagorean Theorem:

`\begin{gathered} \text{adjacent}=\sqrt[]{hypotenuse^2-opposite^2} \\ \\ \text{adjacent}=\sqrt[]{7^2-6^2} \\ \\ \text{adjacent}=\sqrt[]{49-36}=\sqrt[]{13} \end{gathered}`

Apply the definition of tangent to find tanθ:

`\begin{gathered} \tan \theta=\frac{opposite}{\text{adjacent}} \\ \\ \text{tan}\theta=\frac{6}{\sqrt[]{13}} \end{gathered}`

Simplify:

`\begin{gathered} \tan \theta=\frac{6}{\sqrt[]{13}}*\frac{\sqrt[]{13}}{\sqrt[]{13}} \\ \\ \tan \theta=\frac{6\sqrt[]{13}}{13}=1.664 \end{gathered}`

ANSWER:

`\tan \theta=1.664`