Let's put the given details in the figure to better understand the scenario.
For JK and MN to be proven parallel, the following relationship of sides must satisfy:
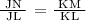
This relationship of sides is under the Triangle Proportionality Theorem.
Under this theorem, if a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally.
Let's now investigate,
JN = 18
JL = 30
KM = 21
KL = 56
We get,
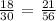
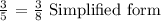
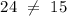
From our investigation, it appears that the sides aren't proportional.
Therefore, JK and MN are not parallel.