we are given the following inequations:
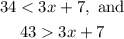
Since both inequalities contain the term "3x + 7" we can use a single inequality of the following form:
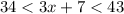
We notice that the direction of the inequality with respect to "3x + 7" remains the same. Now, to solve for "x" we will subtract 7 from the three sides of the inequality:
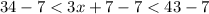
Solving the operations we get:
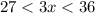
Now we divide the three sides by 3:
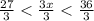
Solving the operations:
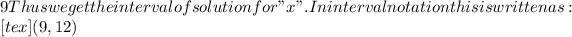
We use parenthesis because the inequality does not present an equal sign.