Given the following function:
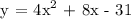
(a) Give the coordinates of the vertex of the graph of the function.
First, let's identify the value of a, b and c.
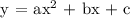
We get,
a = 4
b = 8
c = -31
Let's first the x-coordinate of the vertex.
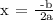
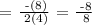

Next, let's find the y-coordinate of the vertex. Substitute x = -1 to the given function.
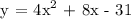
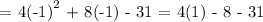
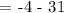
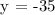
Therefore, the vertex of the graph of the function is at the point -1, -35
Answer: -1, -35
Plotting this into a graph, we get: