Question

C. O(6.913 m, -76.906 m)D. O(6.913 m, -89.798 m)E. O(31.876 m, -76.906 m)15. Given the vectors A = 70 m 50 degnorth of east and B = 40 m 80 degnorth of east, find the magnitude and direction (with respect to the positive x axis)of their sum vector A+ B. (1 point)A. O 106.535 m, 78.383 degB. O 195.912 m, 78.383 degC. O 195.912 m, 60.82 degD. O 106.535 m, 60.82 degE. O 169.689 m, 37.592 degSubmit QueryDaniel Gebreselasie

Answer 1

Given:

The vector A is 70 m 50 deg north of east

The vector B is 40 m 80 deg north of east

To find the magnitude and direction(with respect to the positive x-axis) of the resultant.

Step-by-step explanation:

The vectors can be represented in the diagram as shown below

The x-component of the resultant will be

`\begin{gathered} R_x=70cos(50^(\circ))+40cos(80^(\circ)) \\ =51.941\text{ m} \end{gathered}`

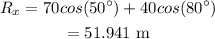
The y-component of the resultant will be

`\begin{gathered} R_y=70sin(50^(\circ))+40sin(80^(\circ)) \\ =93.015\text{ m} \end{gathered}`

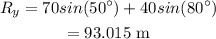
The magnitude of the resultant can be calculated as

`\begin{gathered} R=√(R_x+R_y) \\ =√((51.941)^2+(93.015)^2) \\ =106.535\text{ m} \end{gathered}`

The direction can be calculated as

`\begin{gathered} \theta\text{ =tan}^(-1)((R_y)/(R_x)) \\ =\text{ tan}^(-1)((93.015)/(51.941)) \\ =\text{ 60.82}^(\circ) \end{gathered}`

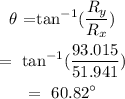
Thus, option D is the correct option.