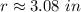Question

The surface area of a sphere is 38 Pi inches squared. What is the radius of the sphere

Answer 1

The surface area of a sphere can be calculated using this formula:

`SA=4\pi r^2`

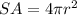
Where "r" is the radius of the sphere.

In this case, knowing that:

`SA=38\pi\text{ }in^2`

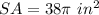
You can substitute this value into the formula and solve for the radius "r". Then, you get:

`\begin{gathered} 38\pi\text{ }in^2=4\pi r^2 \\ \\ \frac{38\pi\text{ }in^2}{4\pi}=r^2 \\ \\ \sqrt[]{\frac{38\pi\text{ }in^2}{4\pi}}=r \end{gathered}`
`r\approx3.08\text{ }in`

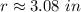
Therefore, the answer is:

`r\approx3.08\text{ }in`