Experimental probability refers to the probability of an event occurring when an experiment was conducted. Mathematically, this can be represented as shown below
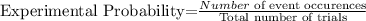
It should be noted that in order for experimental probability to be meaningful in research, the sample size must be sufficiently large. The reason why it is important to use a large number of trials when using experimental probability to predict the result is the law of large numbers.
In statistics and probability theory, the law of large numbers is a theorem that describes the result of repeating the same experiment a large number of times. The large numbers theorem states that if the same experiment or study is repeated independently a large number of times, the average of the results of the trials must be close to the expected value. The result becomes closer to the expected value as the number of trials is increased.
Hence, it is important to use a large number of trials when using experimental probability to predict results because the result becomes closer to the expected value as the number of trials is increased