Question

What is the area of a regular octagon inscribed in a circle of radius 5 meters?

Answer 1

`A)70.711m²`

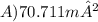
1) We can visualize that regular octagon inscribed this way:

2) We can decompose that regular octagon as isosceles triangles since this the radius is known

But note that we only have the length of the radius:

3) So let's find the base of the triangle, note that the interior angle is:

Finding the height:

Now, let's find the area of one triangle and then multiply by 8 to get the area of the whole Octagon:

`\begin{gathered} AJ=5\cdot\sin(67.5)\Rightarrow AJ\approx4.6194 \\ BJ=5\cdot cos(67.5)\approx1.9134 \\ A_(\Delta)=(1)/(2)\cdot2\cdot(1.9134)\cdot(4.6194)\approx8.83875996 \\ 8\cdot8.8375996\approx70.7007968\approx70.711m² \end{gathered}`