Question

Can you please help with thisAtleast just the first one.

Answer 1

Given:

The function f(x) = ln(x) and g(x) = ln(x + 6).

Required:

Describe how a graph is transformation of the graph of f(x) = ln(x). Also, identify which attributes of f(x) = ln(x) change as a result of the transformation.

Step-by-step explanation:

Let's first gather the required information:

Domain:

The domain of a function is the set of input values for f, in which the function is real and defined.

Range:

The range of a function comprises the set of values of a dependent variable for which the given function is defined.

End behavior:

The end behavior of a function describes the trend of the graph if we look to the right end of the x-axis (as x approcahes +∞) and to the left end of the x-axis (as x approaches −∞).

Vertical asymptote:

x - intercept:

To find the x-intercept, set y = 0 and solve for x.

Now, the graph of f(x) = ln(x) and g(x) = ln(x + 6).

So, graph of f(x) transformed 6 units left on x - axis as a g(x).

`\begin{gathered} Domain: \\ f(x)=(0,\infty) \\ g(x)=(-6,\infty) \end{gathered}`
`\begin{gathered} Range: \\ f(x)=(-\infty,\infty) \\ g(x)=(-\infty,\infty) \end{gathered}`
`\begin{gathered} End\text{ }behavior: \\ f(x): \\ f(x)=ln(x)\rightarrow\infty\text{ as }x\rightarrow\infty\text{ }(ln(x)\text{ grows without bound as x grows} \\ \text{ without bound and }f(x)=ln(x)\rightarrow-\infty\text{ as }x\rightarrow0^{+\text{ }}\text{ }(ln(x)\text{ grows } \\ \text{ without bound in the negative direction as x approaches zero from the} \\ \text{ right\rparen.} \\ g(x): \\ as\text{ }x\rightarrow\infty,\text{ }f(x)\rightarrow+\infty \end{gathered}`

`\begin{gathered} Vertical\text{ }asymptote: \\ f(x): \\ \text{ No vetical asymptotes.} \\ g(x): \\ \text{ No vertical asymptotes. } \end{gathered}`
`\begin{gathered} X-intercept: \\ f(x): \\ (1,0) \\ g(x): \\ (-5,0) \end{gathered}`
`\begin{gathered} \text{ Check where function is positive and negeative:} \\ f(x): \\ \text{ Function is negative for interval }(0,1)\text{ and positive in interval }(1,\infty). \\ g(x): \\ \text{ Function is negative for interval }(-6,-5)\text{ and positive for interval }(-5,\infty). \end{gathered}`
`\begin{gathered} \text{ Check where function increases or decreases}:\text{ } \\ f(x): \\ \text{ Function increases for interval }(0,\infty). \\ g(x): \\ \text{ Function increases for interval }(-6,\infty). \end{gathered}`

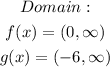
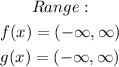
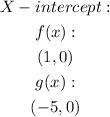
Answer:

Completed answering the question.