As per given by the question,
There are given that,
The confidence interval is 95%, standard deviation is $0.45, and the margine of error is $0.14.
Now,
From the confidence interval 95%,
Here,
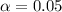
Because of according to the z-score table,
There are given that in the form of row and column.
Now,
The value of Z of given confidence interval is,
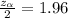
Now,
Find the sample size n;
So,
The formula of the sample size n is,
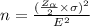
Then,
Put the all given value in above formula,
So,
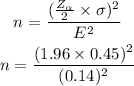
Then,
Find the value of n from above equation;
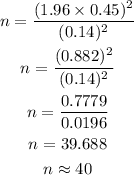
Hence, the pizza shop owner needs $40.