fromAre you the question;
we will be solving for
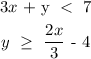
Solving the first inequality
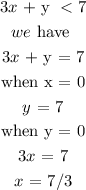
Therefore,
For the first inequality
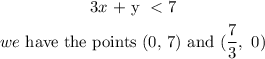
For the second inequality
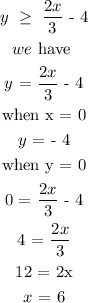
Therefore,
For the second inequality
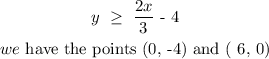
We will be plotting the graph of the inequalities using the appropriate points
The graph above shows the graph of the inequalities
The overlapping region(purple region) shows the solution of the inequalities