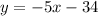Question

Find the equation of the linear function represented by the table shown in slope-interceptform.

Answer 1

Given the table:

x y

-6 -4

-5 -9

-4 -14

-3 -19

-2 -24

Let's find the equation of the linear function reresented by the table shown in slope-intercept form.

Apply the slope-intercept form of a linear equation:

y = mx + b

Where m is the slo and b is the y-intercept.

To find the slope, apply the slope formula:

`m=(y2-y1)/(x2-x2)`

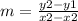
Take any two points on the line:

(x1, y1) ==> (-6, -4)

(x2, y2) ==> (-5, -9)

Thus, we have:

`\begin{gathered} m=(-9-(-4))/(-5-(-6)) \\ \\ m=(-9+4)/(-5+6) \\ \\ m=(-5)/(1) \\ \\ m=-5 \end{gathered}`

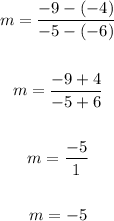
The slope (m) = -5.

To find the y-intercept, substitite for -5 for m, then input the values of any point for x and y in (y = mx + b).

Take the point:

(x, y) ==> (-6, -4)

Hence, we have:

y = mx + b

-4 = -5(-6) + b

-4 = 30 + b

Subtract 30 from both sides:

-4 - 30 = 30 - 30 + b

-34 = b

b = -34

The y-intercept, (b) = -34.

To write the equation, subsutitute -5 for m and -34 for b in (y = mx + b)

Hence, the equation of the line is:

y = -5x - 34

ANSWER:

`y=-5x-34`