Question

Hello I need help on this question The Final Answer requires it to be rounded to the nearest hundred

Answer 1

Given

A training field is formed by joining a rectangle and two semi-circles.

The dimensions of the rectangle is 80m and 68m.

To find: The area of the training field.

Step-by-step explanation:

It is given that,

The length of the rectangle is 80m.

The breadth of the rectangle is 68m.

Also, the radius of the semicircle is,

`\begin{gathered} r=(68)/(2) \\ r=34m \end{gathered}`

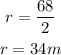
Therefore, the area of the training field is,

`\begin{gathered} Area\text{ }of\text{ }the\text{ }training\text{ }field=Area\text{ }of\text{ }rectangle+2* Area\text{ }of\text{ semicircle} \\ =(80*68)+2*(1)/(2)*(22)/(7)*(34)^2 \\ =5440+3633.142857142 \\ =9073.142857142 \\ =9073.14m^2 \end{gathered}`

Hence, the area of the training field is 9073.14m^2.