Question

Given Angle GFZ equals 42 degrees, Angle ZFE equals 3x + 10, and Angle GFE equals 5x +4, find x

Answer 1

To determine the value of x, you have to apply the angle addition postulate, which states that if you construct an angle by putting two angles together (so that they share one side and the vertex), the measure of this angle will be equal to the sum of the measures of the two original angles.

In this case, this means that the measure of ∠GFE is equal to the sum of ∠GFZ and ∠ZFE:

`\angle\text{GFE}=\angle\text{GFZ}+\angle\text{ZFE}`

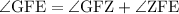
We know that

∠GFE= 5x+4

∠GFZ= 42º

∠ZFE= 3x+10

Then we can determine the following expression:

`(5x+4)=42+(3x+10)`

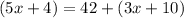
From this equation, we can determine the value of x,

-First, remove the parentheses and simplify the like terms:

`\begin{gathered} 5x+4=3x+42+10 \\ 5x+4=3x+52 \end{gathered}`

-Second, pass "4" to the right side of the equation and "3x" to the left side of the equation by applying the opposite operation to both sides of it:

`\begin{gathered} 5x+4-4=3x+52-4 \\ 5x=3x+48 \end{gathered}`
`\begin{gathered} 5x-3x=3x-3x+48 \\ 2x=48 \end{gathered}`

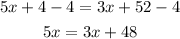
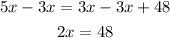
-Third, divide both sides of the equation by 2 to reach the value of x:

`\begin{gathered} (2x)/(2)=(48)/(2) \\ x=24 \end{gathered}`

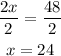
The value of x is 24.