Question

What annual rate of return is earned on a $14,000 investment when it grows to $20,000 in four years?9.11 percent9.43 percent9.01 percentO 9.33 percent

Answer 1

4th option: 9.33 percent

Explanation:

We have that the compound interest formula is the following:

`I=A\left(1+(r)/(100)\right)^t`

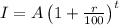
Where I is the interest payment, A is the initial invested value, r is the rate and t is the time in this case in years.

Therefore, we substitute and calculate the annual rate, like this:

`\begin{gathered} 20000=14000\left(1+(r)/(100)\right)^4 \\ \\ 14000\left(1+(r)/(100)\right)^4=20000 \\ \\ \left(1+(r)/(100)\right)^4=(20000)/(14000) \\ \\ \left(1+(r)/(100)\right)^4=(10)/(7) \\ \\ 1+(r)/(100)=\sqrt[4]{(10)/(7)} \\ \\ (r)/(100)=\sqrt[4]{(10)/(7)}-1 \\ \\ r=100\sqrt[4]{(10)/(7)}-100 \\ \\ r=9.326\cong9.33\% \end{gathered}`

So the correct answer is 4th option: 9.33 percent