Question

I need help with this problem and when solving it can you go in depth on how to balance this equation.

Answer 1

Firstly, the equation needs to be balanced.

Let's start by balancing Na, which we can do by adding the coefficient 2 to NaNO₃

`Na_2S+Cu(NO_3)_2\to2NaNO_3_{}+CuS`

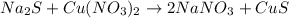
Now, we can check for the other elements.

Cu and S are balanced and the group NO3 is also balanced, so N and O are balanced.

Now, with the balanced equation, we need to consult the molar masses of NaNO₃ and Na₂S, which can be calculated from the molar masses of the elements on them:

`\begin{gathered} M_{NaNO_(3)}\approx84.99467g\/mol \\ M_{Na_(2)S}\approx78.04454g\/mol \end{gathered}`

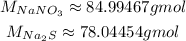
Now, we first convert the mass of NaNO₃ to number of moles:

`n_(NaNO_3)=\frac{m_(NaNO_3)}{M_{NaNO_(3)}}=(75.19g)/(84.99467\/mol)=0.884643\ldots mol`

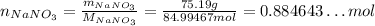
Since the stoichiometry of Na₂S and NaNO₃ is 1 : 2, if we want 0.884643...mol of NaNO₃, we need half as much of Na₂S:

`\begin{gathered} (n_(Na_2S))/(1)=(n_(NaNO_3))/(2) \\ n_(Na_2S)=(0.884643\ldots mol)/(2)=0.442321\ldots mol \end{gathered}`

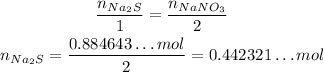
And now, we convert it to mass of Na₂S:

`m_(Na_2S)=n_(Na_2S)\cdot M_(Na_2S)=0.442321\ldots mol\cdot78.04454g\/mol=34.5208\ldots g`

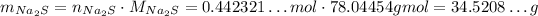
Now, we need to round to 4 significant figures:

`m_{Na_(2)S}\approx34.52g`

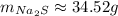
So, the answer is 34.52g of NaNO₃.