Question

Delta has decided to start a side business as a photographer. She purchases a camera for $1600 but it loses value at 12.5% per year. How much will her camera be worth after 5 years? Round to the nearest cent.

Answer 1

Given:

Initial value of camera = $1600

Percentage decrease = 12.5% per year = 0.125

Time, t = 5 years

Let's find the value of the camera after the given time (5 years).

To find the value of the camera, apply the exponential decay formula:

`A=P(1-r)^t`

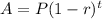
Where:

A is the final value

P is the initial value = $1600

r is the rate of change = 0.125

t is the time = 5 years

Thus, we have:

`\begin{gathered} A=1600(1-0.125)^5 \\ \\ A=1600(0.875)^5 \\ \\ A=1600(0.5129) \\ \\ A=820.65 \end{gathered}`

Therefore, the value of the camera after 5 years will be $820.65

ANSWER:

$820.65