Question

This is an old practice assignment that I don’t understand.

Answer 1

From the grid provided in the picture, we have been given the following coordinates of these places

Sun Bank (1, 7)

Cleaners (15, 4)

Community Garden (20, 0)

We are told to calculate

(a) the slope of Moonbeam drive

The slope of Moonbeam drive is the slope of the line that represents Moonbeam drive. This line has two places (Cleaners and Community garden), with coordinates of (15, 4) and (20, 0) respectively. We will use these points to determine the slope of Moonbeam drive. This becomes

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \text{Where m = slope } \\ x_1=15,y_1=4,x_2=20,y_2=0 \end{gathered}`

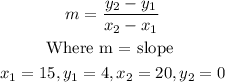
Substituting the values we have

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=\frac{0_{}-4_{}}{20_{}-15_{}} \\ m=(-4)/(5) \\ m=-(4)/(5) \end{gathered}`

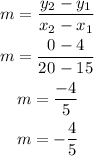
Hence, the slope of Moonbeam drive is

`m=-(4)/(5)`

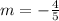
2. Equation of the line that represents Moonbeam drive?

Equation of a line in Point-slope form is given as

`y-y_1=m(x-x_1)`

We can take a point with x and y coordinates to do this, let's take the point Cleaners (15, 4)

So,

`x_1=15,y_1=4`

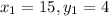
The equation becomes

`\begin{gathered} y-y_1=m(x-x_1) \\ y-4_{}=(-4)/(5)(x-15) \end{gathered}`

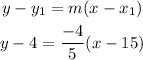
Hence, the equation in Point-slope form is

`y-4_{}=(-4)/(5)(x-15)`

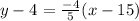
If we simply this further, we will get the equation in slope-intercept form

Because equation in slope-intercept form is given as

`\begin{gathered} y=mx+b \\ \text{where m is slope and b is the intercept on the y-axis } \end{gathered}`

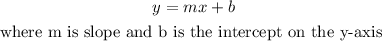
So, simplifying the equation in point-slope form we have

`\begin{gathered} y-4_{}=(-4)/(5)(x-15) \\ y-4=-(4)/(5)x+12 \\ y=-(4)/(5)x+12+4 \\ y=-(4)/(5)x+16 \end{gathered}`

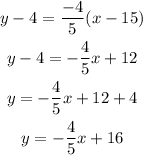
Hence, the equation in slope-intercept form is

`y=-(4)/(5)x+16`

3. The slope of Sunshine Avenue?

We have been told that Moonbeam drive and Sunshine Avenue are two roads that are parallel to each other, so that means that the lines that represent Moonbeam drive and Sunshine Avenue are two parallel lines. When two lines are parallel, they have equal slopes, hence the slope of the line Sunshine Avenue is

`-(4)/(5)`

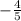
The reason is that the lines Moonbeam drive and Sunshine Avenue are parallel, hence have equal slopes

4. He wants to build a new dinner located 7 blocks North of Community Garden.

Now, from the point Community garden, count 7 lines above and mark a point.

Hence the Coordinates of New dinner is (20, 7)

I will send you a picture showing the point New dinner and the road Stargazer Boulevard

My line is not straight. Count another 7 lines above Moonbeam drive and draw a straight-line to join the point New dinner