Mean)
In general, the formula is
![\operatorname{mean}=\frac{\text{ sum of elements in the dataset}}{\text{ number of elements in the dataset}}]()
Thus, in our case,
![\begin{gathered} \Rightarrow X=\operatorname{mean}=(4.85+5.10+5.50+4.75+4.5+5+6)/(7) \\ \Rightarrow X=\operatorname{mean}=5.1 \end{gathered}]()
Thus, the mean is 5.1
Variance)
In general, the formula is
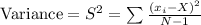
Where x_i is each of the elements in the data set, X is the mean, and N is the number of elements in the data set.
Therefore, in our case,
![\begin{gathered} N=7,X=5.1 \\ \Rightarrow S^2=(1)/(7-1)((4.85-5.1)^2+(5.1-5.1)^2+(5.5-5.1)^2+(4.75-5.1)^2+(4.5-5.1)^2+(5-5.1)^2+(6-5.1)^2) \\ \Rightarrow S^2=0.2541666\ldots \\ \Rightarrow S^2\approx0.254 \end{gathered}]()
The variance is 0.254
Standard deviation)
If S^2 is the variance; then,
![\text{ standard deviation}=\sigma=\sqrt[]{S^2}](https://img.qammunity.org/2023/formulas/mathematics/college/lo96wp4spd0r2fcd1x5n24f1qirmif5sdl.png)
Hence, in our case,
![\begin{gathered} \Rightarrow\sigma=\sqrt[]{0.2541666\ldots}\approx0.504149\ldots \\ \Rightarrow\sigma\approx0.504 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pslausv4an8rezz19utkgko80wxx8cfnqi.png)
The standard deviation is 0.504