Question

1.Ebony kept her bank account open for only 3 weeks, and the graph shows the entire 3 weeks. During that time, her greatest balance was $400.(a)Give the domain and range of the function.(b)Give an estimate to the nearest hundreds for B(0) . Explain how you determined your estimate and tell what means in context of the situation.(c)Ebony’s bank balance first reached $0 on Day 12. How would you show that information in function notation?(d)Ebony’s bank balance remained at $0 from Day 12 through Day 15. As you count segments from the left, which segment on the graph1, 2, 3, 4, 5, or 6 represents that information? Explain how you know.

Answer 1

Given:

Number of weeks = 3 weeks

Greatest balance = $400

The given graph shows the balance for the entire 3 weeks.

Let's solve the for the following:

(a) The domain and range.

• The domain of a graph is the set of all x-values.

Here, the number of days is represented on the x-axis.

Thus, we have:

Number of days in a week = 7 days

Number of days in 3 weeks = 7 x 3 = 21 days.

Therefore, the domain of the function is:

`0\le d\le21`

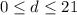
In interval notation, the domain is:

`\lbrack0,21\rbrack`

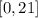
The range of the function is the set of all y-values.

Here, the balance is represented on the y-axis.

Therefore, the range of the function is:

`0\le B\le400`

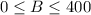
The range in interval notation is:

`\lbrack0,400\rbrack`

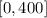
• (b). Give an estimate for B(0).

Here we are to find balance when at day 0.

From the graph, let's take the estimate since the values are not written.

When x = 0, y = 200.

Therefore, we have:

B(0) = 200

B(0) is 200 because we can see when D = 0, the graph is at half the highest point of the balance.

Since the highest balance was $400, B(0) will be half of the $400.

• (c) Where EBony's balance reached $0 on day 12. Let's show this information in function notation.

In function notation, when D = 12, B = 0, we have:

B(12) = 0

• (D) Given that the account remained $0 from day 12 through 15. Let's determine the segment that represents the information.

Here, we can see that when the balance is $0, the graph is flaton the x-axis.

It means y = 0.

Therefore the segment that represents this information is segment 4.

ANSWER:

• (a) Domain: [0, 21]

Range: [0, 400]

• (b) B(0) = 200

• (c) B(12) = 0

• (d) Segment 4