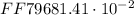We will investigate the process of expressing an algebraic expression in a scientific notation.
We are given the following algebraic expression:
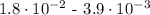
The standard form of the scientific notation is as follows:
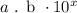
Where,
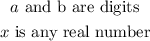
We will construct a step-wise process to determine the above form.
Step 1:- Rationalize the powers of ( 10 )
The first step deals with determination of the common power of each number part of the expression. For this step we will determine the lowest power amoung ( 10^-2 ) and ( 10^-3 ). Such as follows:
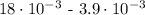
We moved the decimal place to the right for thr first number and subtracted ( 1 ) from its power of ( 10 ). This way both the numbers now have the same powers of ( 10 ).
Step 2:- Factor out the powers of ( 10 )
Next step deals with the factorization of the entire expression based on the commonality of power of ( 10 ) which was constructed in Step 1. We will go ahead and factor out the power of ( 10 )s as follows:

Step 3:- Apply the basic mathematical operation
The factor inside the parenthesis consists only of integers which can be further simplified with the help of a basic mathematical operation of " subtraction ":
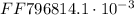
Step 4:- Conversion to standard scientific notation
We will now compare the answer we arrived at in Step 4 and the standard form of scientific notation given initially. We see that the standard form is categorized by the decimal place right after the first digit. However, the answer we arrived at has a decimal place after two digits.
The conversion merely involves the placement of decimal and its applicable correction in powers of 10. If we were to move the decimal place to the left then we add ( 1 ) to the power of ( 10 ) for each digit crossed, whereas moving a decimal place to the right then we subtract ( 1 ) from the power of ( 10 ) for each digit crossed.
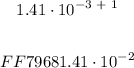
The above form is the simplified result of the algebraic expression in scientific notation and as follows: