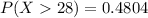Question

Commute Time to Work The average commute to work (one way) is 25 minutes according to the 2005 American Community Survey. If we assume thatcommuting times are normally distributed and that the standard deviation is 6.1 minutes, find the probabilities.(a) The selected commuter spends more than 28 minutes commuting one way.(a) The selected commuter spends more than 28 minutes commuting one way.P(X>28) =

Answer 1

From the given information, we know that

In order to find the probability, we need to find the z-score for the measure X=28. The z-score formula is given by

`z=(X-\mu)/(\sigma)`

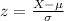
By substituting the given values, we have

`\begin{gathered} z=(28-25)/(61) \\ z=(3)/(61) \\ z=0.04918 \end{gathered}`

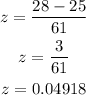
Now, we need to find the p-value corresponding to this z-value. Then, we found that

`P(z>0.04918)=0.48039`

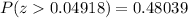
Therefore, by rouding to 4 decimal places, the answer is

`P(X>28)=0.4804`