Question

Is this the graph of g(x)=-x^4(x+3) or h(x)=x^4(x+3)? Explain how you know.

Answer 1

Given the following functions:

`\begin{gathered} g\mleft(x\mright)=-x^4\mleft(x+3\mright) \\ \\ h\mleft(x\mright)=x^4\mleft(x+3\mright) \end{gathered}`

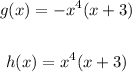
You can identify that the degree is of both functions is:

`Degree\colon5`

Because, if you apply Distributive Property:

`\begin{gathered} g(x)=-x^5-3x^4 \\ \\ h(x)=x^5+3x^4 \end{gathered}`

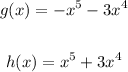
The Leading Coefficient is the coefficient of the variable with the highest degree.

In this case, you can identify that the Leading Coefficient of the function g(x) is negative and the Leading Coefficient of the function h(x) is positive. Then, knowing this, you can know the end behavior of the functions.

Analyzing the graph given in the exercise, you can identify that its ends head off in opposite directions (because it is an Odd polynomial function).

You can also notice that the end on the left starts in the left top of the Coordinate Plane and the end on the right is in the right bottom of the Coordinate Plane. This happens when the Odd polynomial function has a negative Leading Coefficient.

Therefore, the answer is:

It is the graph of:

`g\mleft(x\mright)=-x^4\mleft(x+3\mright)`

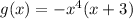
Because it is an Odd polynomial function that has a negative Leading Coefficient.