Given: A series 11,15,19,23,27,...
Required: To determine the nth term.
Explanation: The given series is an arithmetic progression with the first term, a=11, and the common difference, d=4.
The formula gives the nth term of an AP-
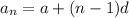
Substituting the values into the formula as-
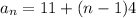
Further solving-

Final Answer: The nth term of the series is 4n+7.