Let's find the equation of the line.
The equation of a line is found by the formula

Where
m is the slope (rise over run)
(x_1, y_1) is a point through which the line passes
The slope can be found just by looking at the graph. We take any 2 points and find the change in y coordinates and divide it by the change in x coordinates.
Let's take (0,0) and (1, 5).
We can see that the change in y coordinates is 5 and the change in x coordinates is 1. Thus, the slope is 5/1 = 5
So, we have
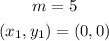
Let's use the formula and find out the equation of the line:
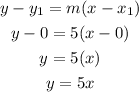
Now, we want to find the number of pizzas (y) Amelia can make in 3 hours (x). We simply plug in "3" into x and solve for y. This is shown below:
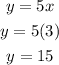
So, Amelia can make 15 pizzas in 3 hours.
Answer
15 pizzas